Linear Regression Algorithm

โดย ชิตพงษ์ กิตตินราดร | ธันวาคม 2562

วิธีที่ดีที่สุดในการทำความเข้าใจ Machine learning คือการอธิบายพร้อมกับตัวอย่าง โดยเราจะเริ่มที่ Algorithm ที่ง่ายที่สุด นั่นคือ Linear regression

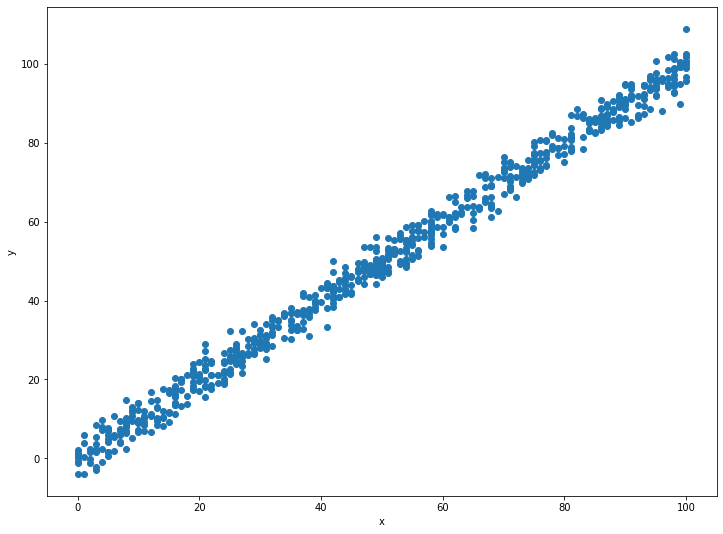
เราจะใช้ข้อมูลตัวอย่างจาก Kaggle ซึ่งแสดงความสัมพันธ์ระหว่างตัวแปร x บนแกนนอนกับตัวแปร y บนแกนตั้ง ถ้ามองด้วยตาเราจะเห็นว่า x กับ y มีความสัมพันธ์ที่เรียกว่า Positive correlation อย่างชัดเจน นั่นคือยิ่ง x มีค่ามาก y ก็มีค่ามากตามไปด้วย เราจะเห็นความสัมพันธ์ลักษณะในโลกจริงได้มากมาย ตัวอย่างเช่น ยิ่งจำนวนรถมาก เวลาที่ใช้บนถนนต่อการเดินทางหนึ่งเที่ยวก็มีแนวโน้มจะมากขึ้นด้วย

ปัจจุบัน ชุดข้อมูลนี้มีค่า x และ y จำนวน 999 คู่ ตัวอย่างเช่น คู่แรก x = 24, y = 21.54 ส่วนคู่ที่สอง x = 50, y = 47.46 เราเรียกข้อมูลแต่ละคู่เช่นนี้ว่าข้อมูลหนึ่งรายการ

จริงอยู่ที่เรามีข้อมูลถึง 999 รายการ แต่ถ้าเราเก็บข้อมูลมาใหม่เป็นรายการที่ 1000 โดยข้อมูลรายการนี้รู้แค่ค่า x เราจะรู้ได้อย่างไรว่าค่า y เป็นเท่าไร

ตัวอย่างเช่น ถ้าข้อมูลใหม่มี x = 22 เราอาจจะลองลากเส้นแนวดิ่งจากแกน x ที่ 22 แล้วไปบรรจบตั้งฉากกับแกน y ซึ่งดูเหมือนจะได้ประมาณ 20 แต่ช้าก่อน มันอาจจะเป็น 18, 25 หรือแม้กระทั่ง 30 ก็ได้ เพราะข้อมูลตัวอย่างของเรามีรายการที่ x มีค่าประมาณ 22 อยู่หลายรายการ ซึ่งแต่ละรายการก็มีค่า y ไม่เท่ากันเลย

Machine learning จึงมาช่วยเราได้ โดยการใช้ Algorithm ซึ่งก็คือสูตรและกลไกทางคณิตศาสตร์ มาเรียนรู้ข้อมูลที่เรามี เพื่อสร้างโมเดลของข้อมูลขึ้นมา เราจะใช้โมเดลที่สร้างขึ้นนี้ ในการพยากรณ์คำตอบ ซึ่งก็คือค่า y ที่เราต้องการ

ซึ่งในกรณีนี้ โมเดลที่ได้คือ:

$$\hat{y} = 1.00065638x - 0.10726546\tag{1}$$

ดังนั้นถ้าเราลองใส่ค่า x = 22 ลงไป จะได้ y = 21.90

คำถามคือ โมเดลนี้ได้มาอย่างไร คำตอบอยู่ในส่วนต่อไป

Hypothesis function

หัวใจของโมเดลพยากรณ์ คือฟังก์ชันคณิตศาสตร์ที่เป็นตัวแทนความสัมพันธ์ระหว่างตัวแปร x กับคำตอบ y เราเรียกฟังก์ชันนี้ว่า Hypothesis function ซึ่งหมายถึงฟังก์ชันที่เป็น "สมมุติฐาน" ว่าข้อมูลมีความสัมพันธ์กันอย่างไรนั่นเอง โดยในปัญหา Linear regression นั้น Hypothesis function จะอยู่ในรูปแบบ:

$$\hat{y} = wx + b\tag{2}$$

• $\hat{y}$ คือค่าคำตอบที่พยากรณ์ได้
• $w$ คือค่าน้ำหนักของตัวแปร x (มาจากคำว่า Weight) ซึ่งกำหนดความชันของฟังก์ชัน
• $x$ คือตัวแปร x ที่เรารู้ค่า
• $b$ คือจุดตัดแกน y (มาจากคำว่า Bias)

ฟังก์ชันนี้อยู่ในรูปแบบสมการเส้นตรง นั่นคือค่า x ที่ใส่ลงไป จะมีความสัมพันธ์กับค่า y แบบที่ลากเป็นเส้นตรงได้

หน้าที่ของ Machine learning คือการหาตัวแปร w และ b ซึ่งจะประกอบกันเป็น Hypothesis function ที่มีความคลาดเคลื่อนน้อยที่สุดเมื่อเทียบกับข้อมูลที่เรามี ซึ่งในกรณีตัวอย่างนี้ เราได้ w = 1.00065638 และ b = -0.10726546

เรารู้ได้อย่างไรว่า w และ b ต้องมีค่าเท่าใดจึงจะทำให้โมเดลมีความคลาดเคลื่อนน้อยที่สุด คำตอบมีอยู่ 2 ส่วน ส่วนแรกคือเราต้องมีวิธีการวัดความคลาดเคลื่อน ซึ่งเรียกว่า Cost function ส่วนที่สองคือเราต้องมีวิธีการหาค่า w และ b ที่จะทำให้ค่าความคลาดเคลื่อนใน Cost function นั้นต่ำที่สุด เรียกกระบวนการนี้ว่า Gradient descent

Cost function

สำหรับ Hypothesis function แต่ละฟังก์ชัน จะมี Cost function คู่อยู่เสมอ ซึ่งทำหน้าที่วัดว่าค่า y ที่พยากรณ์ได้จาก Hypothesis function มีความคลาดเคลื่อนกับค่า y ที่เรามีข้อมูลอยู่จริงเท่าใด โดยสำหรับ Linear regression เราใช้ฟังก์ชันต่อไปนี้เป็น Cost function:

$$J(w, b) = \frac{1}{2m} \sum\limits_{i = 1}^m(\hat{y}_i - y_i)^2\tag{3}$$

• $J(w, b)$ คือผลความต่างระหว่างค่าพยากรณ์กับค่าจริง ที่สอดคล้องกับตัวแปร w และ b
• $m$ คือจำนวนรายการข้อมูลทั้งหมดที่มี (เช่นในกรณีตัวอย่างนี้ m = 699 มาจากข้อมูล 999 รายการ แต่กัน 300 รายการเอาไว้ทดสอบความแม่นยำ เรื่องนี้จะอธิบายภายหลัง)
• $\sum\limits_{i = 1}^m$ คือผลรวมของรายการถัดไป โดยรวมจากรายการที่ 1 ถึงรายการที่ m
• $(\hat{y}_i - y_i)^2$ คือผลต่างระหว่างค่า y ที่พยากรณ์ได้ กับค่า y จริง ของแต่ละรายการ แล้วนำไปยกกำลัง 2 ตัวอย่างเช่น ถ้ารายการแรก พยากรณ์ได้ 20 แต่ในความเป็นจริงต้องเป็น 21.54 จะได้ผลต่างยกกำลัง 2 เท่ากับ $(20-21.54)^2 = 2.37$

อนึ่ง ฟังก์ชันนี้ มีชื่อเรียกเฉพาะตัว ว่า Mean Squared Error หรือ MSE

เป้าหมายของ Algorithm คือการทำให้ $J(w, b)$ มีค่าต่ำที่สุดเท่าที่จะเป็นไปได้ เราเรียกจุดนี้ว่า Global minimum ซึ่งหาได้โดยใช้กระบวนการที่เรียกว่า Gradient descent

Gradient descent

ทบทวนอีกครั้งว่าเรามี Cost function ที่กำหนดความสัมพันธ์ระหว่างตัวแปร w, b กับความคลาดเคลื่อนของโมเดล ในโมเดลที่ข้อมูลมีมิติเดียว (คือมี x เพียงหนึ่งตัวสำหรับข้อมูลแต่ละรายการ แต่ละ x ก็มี w เพียงตัวเดียวเป็นค่าน้ำหนัก) รูปร่างของ Cost function จะมีลักษณะเป็นเหมือนชาม คือมีจุดต่ำที่สุด ซึ่งจุดนั้นเป็นจุดที่เราต้องการเนื่องจากจะทำให้ได้ค่าความคลาดเคลื่อนที่ต่ำที่สุด หน้าที่ของ Gradient descent คือการหาตัวแปร w และ b ที่จะทำให้ได้ J ที่ต่ำที่สุด

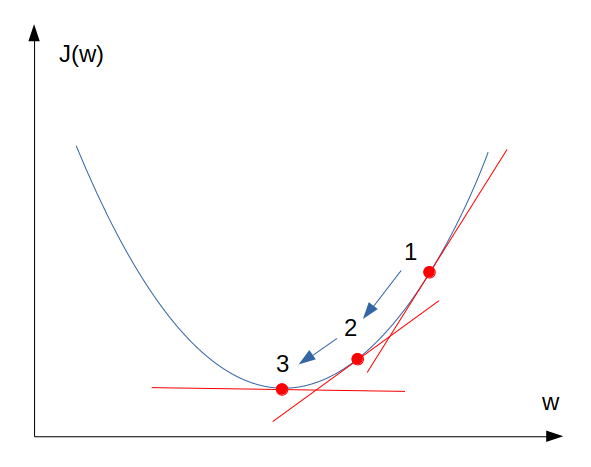
ในที่นี้เราจะพิจารณาเฉพาะ Cost function ของ $J(w)$ ซึ่งผันแปรตามตัวแปร w เพียงตัวเดียวก่อน

การทำงานของ Gradient descent ใช้ประโยชน์จากข้อเท็จจริงที่ว่า ในแต่ละจุดของเส้นฟังก์ชัน $J(w)$ เราจะสามารถลากเส้นไปแตะเพื่อชี้วัด "ความชัน" ของจุดนั้นๆ ได้ จากภาพเราจะเห็นว่าจุดที่ 1 มีความชันมากกว่าจุดที่ 2 และจุดที่ 2 ก็ชันมากกว่าจุดที่ 3 จากคุณสมบัตินี้ หากเรามีกลไกที่จะหาจุดที่มีความชันน้อยลงเรื่อยๆ ไปจนถึงจุดที่แทบไม่มีความชันเลย (จุดที่ 3) เราก็จะได้ Global minimum ที่เราต้องการ

การหาความชันทำได้ด้วยวิชา Calculus โดยการหาอนุพันธ์ (Derivative) ของฟังก์ชัน $J(w)$ เมื่อเปรียบเทียบกับ w ซึ่งแทนเป็นสัญลักษณ์ได้ด้วย:

$$\frac{\partial J(w)}{\partial w}\tag{4}$$

จากวิชา Calculus เราหาอนุพันธ์ของฟังก์ชันดังกล่าว จะได้ Algorithm ทั่วไปคือ:

ทำซ้ำจนกระทั่งผลลัพธ์ล่าสุดไม่เปลี่ยนแปลงจากผลลัพธ์ครั้งก่อน:

$$\theta_j := \theta_j - \alpha \frac{\partial}{\partial\theta_j} J(\theta_0, \theta_1)\tag{5}$$

• $\theta$ อ่านว่า Theta คือตัวแปรต่างๆ ของโมเดล เช่น b, w
• $j$ คือลำดับที่ของตัวแปร โดยจุดตัดแกน y หรือ b อยู่ลำดับที่ 0 ส่วน w อยู่ลำดับที่ 1
• $\alpha$ อ่านว่า Alpha คือค่าคงที่ที่กำหนดอัตราความเร็วของการเคลื่อนที่ไปสู่จุดที่ความชันน้อยลง

จาก Algorithm ทั่วไปนี้ นำมาประยุกต์กับ Linear regression จะได้ว่า:

ทำซ้ำจนกระทั่งผลลัพธ์ล่าสุดไม่เปลี่ยนแปลงจากผลลัพธ์ครั้งก่อน:

$$b := b - \alpha \frac{1}{m} \sum\limits_{i = 1}^m(\hat{y_i} - y_i)\tag{6}$$

$$w := w - \alpha \frac{1}{m} \sum\limits_{i = 1}^m(\hat{y_i} - y_i)x_i)\tag{7}$$

มาลองทำความเข้าใจ Algorithm นี้ด้วยตัวอย่าง สมมุติว่าเราเริ่มคำนวนด้วยค่าตั้งต้นดังนี้: $\theta_0 = b = 2$; $\alpha = 0.5$ ถ้าเราหาอนุพันธ์ครั้งแรกได้ 1 ครั้งที่สองได้ 0.7 และครั้งที่สามได้ 0.4 เราจะได้:

$$2 := 2 - (0.5)1 = 1.5\tag{8}$$

$$1.5 := 1.5 - (0.5)0.7 = 1.15\tag{9}$$

$$1.15 := 1.15 - (0.5)0.4 = 0.95\tag{10}$$

จะเห็นว่า ผลลัพธ์ค่า b ที่ได้มาค่าน้อยลงเรื่อยๆ คือจาก 1.5 เป็น 1.15 เป็น 0.95 โดยผลลัพธ์ที่ได้แต่ละรอบจะส่งผลให้ความชันของ Cost function ลดลงเรื่องๆ ทำให้อนุพันธ์น้อยลงเรื่อยๆ จาก 1 เป็น 0.7 เป็น 0.4 เป็นต้น

เป้าหมายของกระบวนการ Gradient descent นี้คือการหาค่าตัวแปรของโมเดลที่ทำให้โมเดลมีผลลัพธ์ y ที่คลาดเคลื่อนกับค่า y ที่แท้จริงให้น้อยที่สุด นั่นคือเราจะได้โมเดลที่เป็นตัวแทนของชุดข้อมูลนี้ได้ดีที่สุดนั่นเอง

ถ้าสังเกตดีๆ จะเห็นว่า เราสามารถควบคุมกระบวนการนี้ได้ด้วยการกำหนดตัวแปรสองสิ่ง เราเรียกตัวแปรที่เราเป็นผู้กำหนดเองนี้ว่า Hyperparameter ซึ่งในกรณีนี้ ประกอบด้วย:

• $N_{iteration}$ จำนวนครั้งที่เราคำนวนและอับเดตค่าใน Algorithm เช่น 100 ครั้ง หมายความว่าจะมีการคำนวนเพื่อลดความชันลงเรื่อยๆ 100 รอบ โดยถ้าจำนวนครั้งนี้น้อยเกินไป Algorithm ก็จะยังคำนวนไปไม่ถึงจุดที่จะได้ Cost ที่ต่ำที่สุด แต่ถ้าจำนวนครั้งนี้มากเกินไป ก็จะเสียเวลาและพลังงานในการคำนวนมากโดยไม่จำเป็น เพราะรอบหลังๆ ที่ได้ทำให้ Cost function เปลี่ยนแปลง
• $\alpha$ เรียกว่า Learning rate หรืออัตราความเร็วในการอับเดตค่าความชัน (อนุพันธ์ของ J เมื่อเทียบกับตัวแปร) ถ้า Learning rate มีค่ามาก จะทำให้ค่าความชันส่งผลไปยังค่าของตัวแปรมากขึ้น ทำให้โมเดลหาจุด Global minimum ได้เร็วขึ้น ในทางกลับกัน ถ้า Learning rate น้อย ตัวแปรก็จะเปลี่ยนแปลงช้าลง

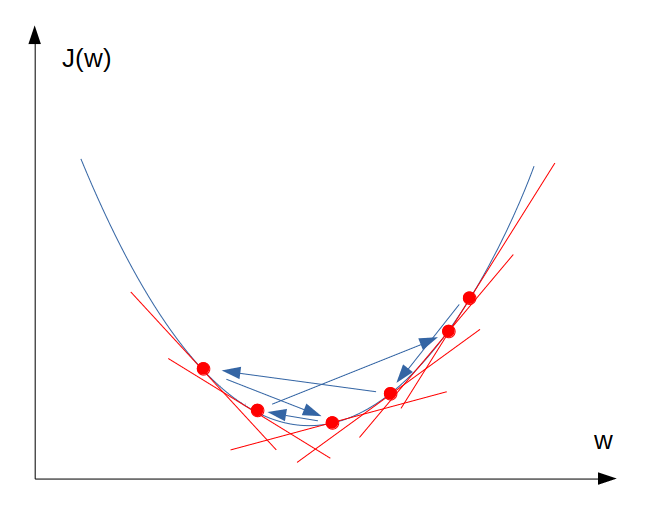
ทีนี้ดูเหมือนกับว่า ถ้าเรากำหนด Learning rate สูงๆ ก็จะทำให้ได้ค่า Global minimum ของ Cost function เร็วขึ้น อย่างไรก็ตามถ้าค่า Learning rate สูงเกินไป อาจจะทำให้โมเดลหา Global minimum ไม่เจอ เพราะในขั้นท้ายๆ ของ Gradient descent ตัวแปรอาจจะกระโดดเลยจุดต่ำสุดของ J ไปอีกด้านหนึ่ง เพื่อความเข้าใจลองดูภาพประกอบ:

Normal equation

นอกจากวิธี Gradient descent แล้ว เรายังมีวิธีการหา Parameter $\theta$ ที่ให้ Cost ที่ต่ำที่สุดอีกวิธี เราเรียกวิธีนี้ว่า Normal equation โดยเพียงใช้สมการ:

Normal equation ทำงานได้ดีและเร็วเมื่อจำนวน Feature ไม่มาก ผู้สนใจสามารถหาอ่านวิธีการ Derive ให้ได้มาซึ่ง Normal equation นี้ด้วยตนเอง

ตอนนี้เรามีความรู้และเข้าใจขั้นตอนการสร้างโมเดล Linear regression แล้ว ตอนถัดไปเราจะใช้ตัวอย่างนี้มาสร้างโมเดลจริงกัน

หน้าแรก | บทที่ 1 บทนำ | บทที่ 3 Linear Regression Programming