Categorical Encoding

โดย ชิตพงษ์ กิตตินราดร | ธันวาคม 2562

ในบทนี้เราจะเริ่มมาเจาะลึกในรายละเอียด โดยจะอธิบายเรื่องการเตรียมข้อมูลให้มีความพร้อมสำหรับการสร้างโมเดล

เราได้ลองสร้าง Machine learning model มาสองเรื่องแล้ว ถ้าสังเกตว่าพบว่า ข้อมูล Input x นั้นจะต้องเป็นตัวเลข แต่ในความเป็นจริง เรามักได้ข้อมูลมาเป็นข้อความ เช่น [ใช่, ไม่ใช่] หรือ [น้อย, กลาง, มาก] ถ้าเรามีข้อมูลแบบนี้ เราจะต้องแปลงข้อมูลที่เป็นข้อความหรือหมวดหมู่ ให้เป็นตัวเลขเสียก่อน

สมมุติเรามีข้อมูลรายได้ ระดับความสุข ภูมิภาคที่อาศัย และอายุขัย ทั้งหมด 20 ตัวอย่าง เราต้องการพยากรณ์อายุขัยโดยใช้ข้อมูล 3 อย่างแรก:

(แสดง 5 ตัวอย่างแรก)

จะเห็นว่า:

• Income หรือรายได้ เป็นตัวเลขอยู่แล้ว
• Happiness หรือระดับความสุข เป็นหมวดหมู่ มี 3 ค่า คือ [High, Medium, Low]
• Area หรือภูมิภาคที่อาศัย เป็นหมวดหมู่ มี 4 ค่า คือ [BKK, NE, S, N]
• LifeExpectacy เป็นตัวเลขอยู่แล้ว

หน้าที่ของเราคือจะต้องแปลง Happiness และ Area เป็นตัวเลข โดยหลักการมี 2 ขั้น ได้แก่

Factorisation

คือการแทนค่าในแต่ละหมวดด้วยตัวเลขต่างๆ กัน เช่น High = 0, Medium = 1, Low = 2 เป็นต้น โดยเราสามารถแปลงเองใน Excel หรือจะให้ pandas แปลงให้ก็ได้ ลองเขียนโค้ดตั้งแต่เริ่มต้นดังนี้:

import numpy as np
import pandas as pd
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn import metrics
import matplotlib.pyplot as plt

# Load the dataset
df = pd.read_csv("data/life_expectancy.csv")

# Explore
print(df.head())
print(df.info())
print(df.describe())

เราจะเห็นว่า Income และ LifeExpectancy เป็นจำนวนเต็ม (int64) ส่วน Happiness และ Area เป็น object ซึ่งสองตัวนี้เป็นสิ่งที่เราต้องจัดการ

RangeIndex: 20 entries, 0 to 19
Data columns (total 4 columns):
Income            20 non-null int64
Happiness         20 non-null object
Area              20 non-null object
LifeExpectancy    20 non-null int64
dtypes: int64(2), object(2)

จากนั้นให้เลือกเฉพาะคอลัมน์ที่เป็น object แล้วลองดูข้อมูลที่ถูกเลือก

# Limit to categorical data using df.select_dtypes()
df_categories = df.select_dtypes(include=[object])
print(df_categories.head())
print(df_categories.columns)
print(df_categories.shape)

จะได้ Dataframe ใหม่ที่มีคอลัมน์ Happiness และ Area เท่านั้นตามต้องการ และมีมิติ (20, 2)

Index(['Happiness', 'Area'], dtype='object')
(20, 2)

จากนั้นเรียก Class LabelEncoder() ใส่เป็น Argument ของ Method .apply ของ Dataframe ใหม่ของเรา แล้วพ่วง Method .fit_transform เพื่อแปลง scipy sparse matrix ให้เป็น numpy dense matrix ซึ่งอยู่ในรูปแบบที่เราจะใช้

# Create a LabelEncoder object and fit it to each feature in X
X_label = df_categories.apply(LabelEncoder().fit_transform)
print(X_label.head())

ถ้างง บรรทัดนี้คือการสั่งให้ Dataframe ของเราดำเนินการเข้ารหัส Label จากข้อความให้กลายเป็นตัวเลข แล้วแปลงผลลัพธ์ให้อยู่ในรูปแบบที่เอาไปใช้ต่อในการเทรนโมเดลได้

ได้ผลคือ:

   Happiness  Area
0          0     0
1          2     2
2          2     3
3          1     2
4          0     0

ถ้าลองเทียบกลับกับข้อมูลจริง เราจะได้คู่รหัสดังนี้:

• {0: "Happiness-Hi", 1: "Happiness-Lo", 2: "Happiness-Mid"}
• {0: "Area-BKK", 1: "Area-N", 2: "Area-S", 3: "Area-NE"}

จากนั้นไปสู่ขั้นตอนต่อไป คือการเข้ารหัส One-hot encoding

One-hot encoding

ขั้นตอนที่แล้ว เราได้รหัสตัวเลขเดี่ยวๆ แทน Label ของแต่ละคอลัมน์ จริงๆ ดูเหมือนเราน่าจะนำรหัสนี้ไปใช้เป็น Input ของโมเดลได้เลย ซึ่งจริงในบางกรณี อธิบายคือการเข้ารหัสแบบ Factorisation ตัวเลขที่อยู่ใกล้กันจะถูกตีความว่ามี "คุณค่า" ใกล้กัน เช่น 1 กับ 2 ใกล้กันมากกว่า 1 กับ 3 ดังนั้น ถ้าค่าจริงของ 1, 2, 3 มีความสัมพันธ์เชิงคุณค่าที่ต่อเนื่องกัน เราก็สามารถใช้ Factorisation ได้เลย เช่นถ้า 1 แปลว่า "น้อย", 2 แปลว่า "ปานกลาง", และ 3 แปลว่า "มาก" เป็นต้น

แต่ในความเป็นจริง มีหลายกรณีที่ค่าจริงของแต่ละเลขนั้นไม่ได้มีความสัมพันธ์ต่อเนื่องเป็นลำดับขั้นกัน เช่นในกรณีภูมิภาคที่อยู่อาศัย ค่าของแต่ละเลขล้วนมีความหมายของมันเอง และไม่เกี่ยวข้องทางลำดับชั้นกับค่าอื่น

วิธีการแก้ปัญหานี้ คือการใช้ One-hot encoding ซึ่งคือการเข้ารหัสแบบ Binary แทนแต่ละ Label ตัวอย่างเช่น [1, 0, 0, 0] แทน BKK (กทม.), [0, 1, 0, 0] แทน N (ภาคเหนือ) เป็นต้น วิธีการนี้จะทำให้ Label แต่ละอันนั้นเป็นอิสระต่อกัน ทำให้การสร้างโมเดลนั้นแม่นยำมากขึ้น

วิธีการทำ One-hot encoding คือ:

# Create a OneHotEncoder object, and fit it to all of X
X_1hot = OneHotEncoder().fit_transform(X_label).toarray()
print(X_1hot[0:5, :])
print(X_1hot.shape)

ได้ผลคือ:

[[1. 0. 0. 1. 0. 0. 0.]
 [0. 0. 1. 0. 0. 1. 0.]
 [0. 0. 1. 0. 0. 0. 1.]
 [0. 1. 0. 0. 0. 1. 0.]
 [1. 0. 0. 1. 0. 0. 0.]]
(20, 7)

สังเกตว่าการทำ One-hot encoding จะเป็นการขยายจำนวน Feature โดยจำนวนที่ขยาย เท่ากับ ผลรวมของจำนวน Label ที่เป็นไปได้ทั้งหมด ดังนั้นจากตัวอย่างของเรา มี 2 Feature ที่ต้องทำ One-hot encoding, Feature แรกมี 3 Label, Feature ที่สองมี 4 Label ดังนั้นจำนวน Feature ใหม่จึงเท่ากับ 7

คำถามคือ แล้วเราจะเอา Array ใหม่นี้ ไปรวมกับข้อมูลเดิมเพื่อสร้าง Input X ได้อย่างไร คำตอบอบู่ที่ส่วนถัดไป

Re-creating input X

ทบทวนว่าตอนนี้เรามี Dataframe อยู่ 2 ชุด

• df คือ Dataframe ต้นฉบับ มีหัวข้อคือ Income, Happiness, Area, และ LifeExpectancy
• df_1hot คือ Dataframe เฉพาะ Happiness และ Area ที่ถูกเข้ารหัส (และขยายขนาด) ด้วย One-hot encoding แล้ว

ทีนี้เรารู้ว่าการจะเทรนโมเดล เราจะต้องเตรียม Dataframe 2 ชุด คือ X ซึ่งเป็น Input ทั้งหมด และ y ซึ่งเป็น Label คำตอบทั้งหมด จะทำอย่างไรดี? อธิบายไปตอนนี้อาจจะงง ลองมาดูโค้ดแล้วอธิบายด้วยโค้ดดีกว่า:

# Recombine numerical and one-hot dataframes to make X
df_1hot = pd.DataFrame(X_1hot)
X = pd.concat([df["Income"], df_1hot], axis=1, sort=False,)
X.columns = ["Income", 
             "Happiness-Hi", "Happiness-Lo", "Happiness-Mid", 
             "Area-BKK", "Area-N", "Area-S", "Area-NE"]
y = df["LifeExpectancy"]
print(X.head())
print(X.shape)
print(y.head())
print(y.shape)

อธิบายดังนี้:

• เราจะรวม Dataframe เข้าด้วยกัน ดังนั้น ขั้นแรกเราต้องแปลง X_1hot ที่เป็น Array ให้เป็น pandas dataframe ก่อน ตั้งชื่อว่า df_1hot
• จากนั้นเราประกอบ Dataframe ใหม่ที่จะเป็น X ของเรา ด้วยการ "ต่อ" (Concatenate) คอลัมน์ Income ของ df ต้นฉบับ เข้ากับ df_1hot ทั้งหมด โดยกำหนด Argument axis=1 เพื่อให้ต่อออกไปทางแนวนอน
• เพื่อความไม่สับสนและเอาไว้อ้างอิง เราจะตั้งชื่อคอลัมน์ใหม่ให้ Dataframe X ของเรา เช่น รหัสแรกของ Happiness ถ้ามีเลข 1 ตรงนั้น ([1, 0, 0]) แปลว่า Happiness-Hi เป็นต้น
• สุดท้ายก็สร้าง Dataframe y โดยเลือกเฉพาะคอลัมน์ที่เป็นคำตอบ จาก Dataframe df ต้นฉบับ

อย่าลืมตรวจดูว่าผลที่ได้นั้นเป็นไปตามที่เราคิด ด้วยการ print head และ shape ของ X กับ y ออกมาดู

เป็นอันว่าเราได้ Dataframe X และ y ที่พร้อมสำหรับการสร้างโมเดลแล้ว

Model training

เรามาฝึกโมเดล Linear regression กันเลย โดนอย่าลืมแยกข้อมูลออกเป็น Train set กับ Test set ก่อน:

# Split the data into train and test set
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
print("X_train shape is:", X_train.shape)
print("y_train shape is:", y_train.shape)
print("X_test shape is:", X_test.shape)
print("y_test shape is:", y_test.shape)

# Train the model
lr = LinearRegression().fit(X_train, y_train)
coeff_df = pd.DataFrame(lr.coef_, X.columns, columns=['Coefficient'])
print(coeff_df)

พอฝึกแล้ว มาลองดูว่าโมเดลให้คำตอบเป็นค่า Coefficient ของน้ำหนักสำหรับแต่ละ Feature อย่างไร สำหรับ Linear regression หลายตัวแปร หรือที่เรียกว่า Multivariate linear regression นี้ สูตร Linear function คือ:

$$\hat{y} = w_1x_1 + w_2x_2 + w_3x_3 + \dots + w_nx_n\ + b \tag{1}$$

โดย n คือจำนวน Feature ซึ่งในกรณีของเราคือ 8

เราสามารถสร้างตารางแสดงค่า Coefficient ของแต่ละ Feature ได้ด้วย pandas dataframe โดยกำหนดใน Argument ให้ lr.coef_ เป็น Input, ให้ชื่อคอลัมน์ X.columns เป็น Label แกนนอน และตั้งชื่อคอลัมน์โดยการกำหนด columns=['Coefficient'] ได้ผลดังนี้:

               Coefficient
Income            0.000055
Happiness-Hi      8.306516
Happiness-Lo     -8.859939
Happiness-Mid     0.553423
Area-BKK         -9.442937
Area-N            3.505052
Area-S            4.850387
Area-NE           1.087498

จากนั้น เราลองมาดูเลยดีกว่าว่าค่าที่พยากรณ์ได้เทียบกับค่าจริงใน Test set เป็นอย่างไร:

# Make a prediction on test set
y_pred = lr.predict(X_test)
df_pred = pd.DataFrame({'Actual': y_test, 'Predicted': y_pred})
print(df_pred)

เราพยากรณ์ y_pred โดยใช้ X_test เป็น Input เพื่อให้ y_pred ที่ได้ สามารถนำไปเปรียบเทียบกับ y_test ที่เรารู้ค่าอยู่แล้ว เราป้อนทั้งสองตัวเป็น Input ของ pandas dataframe จะได้ผลว่า:

    Actual  Predicted
3       59  63.213900
16      89  74.945451
6       49  60.294754
10      76  82.234579
2       72  69.815254

ผลที่ได้ไม่ไกล แต่ก็ไม่ถึงกับใกล้ เราอยากรู้เพิ่ม จึงลองคำนวนค่าเฉลี่ยของ y_test และ y_pred ดู:

print("Mean of y_test is", np.mean(np.array(y_test)))
print("Mean of y_pred is", np.mean(y_pred))

ได้ผลว่า:

Mean of y_test is 69.0
Mean of y_pred is 70.10078755113827

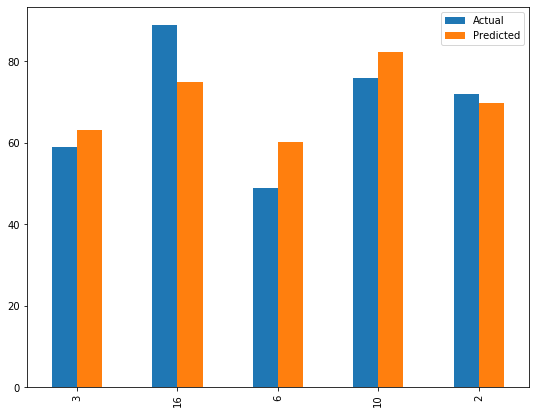
ซึ่งใกล้กันมาก แสดงว่าการพยากรณ์แต่ละรายการ มีความแปรผันมาก เลยลองพล็อตกราฟเทียบให้เห็นๆ:

# Plot the conparison between actual and predicted y
df_pred.plot(kind="bar", figsize=(9,7))
plt.show()

ออกมาดังนี้:

Evaluation metrics

การดูด้วยตาย่อมไม่เพียงพอ เราเลยต้องลองใช้มาตรวัดต่างๆ สำหรับ Linear regression มาวัดดู:

# Evaluate the model
print("Train set R2-score = " + str(lr.score(X_train, y_train)))
print("Test set R2-score = " + str(lr.score(X_test, y_test)))

print('Test set Mean Absolute Error:', metrics.mean_absolute_error(y_test, y_pred))
print('Test set Mean Squared Error:', metrics.mean_squared_error(y_test, y_pred))
print('Test set Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test, y_pred)))

ผลที่ได้มีดังนี้:

Train set R2-score = 0.5401999191488698
Test set R2-score = 0.5965533912121594
Test set Mean Absolute Error: 7.596505622473046
Test set Mean Squared Error: 77.30037024375025
Test set Root Mean Squared Error: 8.792062911726136

อธิบายดังนี้

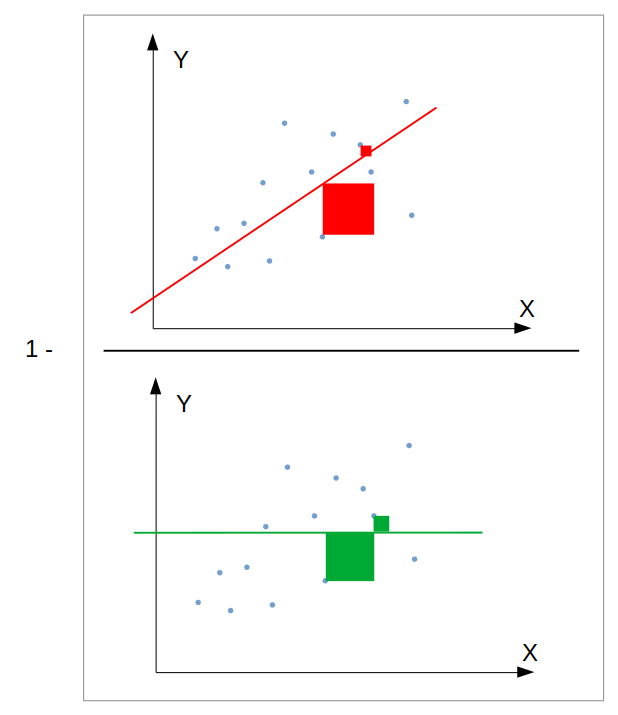
1) $R^2$ Score วัดค่าสะสมของความต่างระหว่างค่าจริงกับค่าที่พยากรณ์ได้ เมื่อเทียบกับค่าสะสมระหว่างค่าจริงกับค่าเฉลี่ยของค่าจริงทั้งหมด:

$$R^2 = 1 - \frac{SS_{res}}{SS_{tot}}\tag{2}$$

$$SS_{res} = \sum\limits_{i = 1}^m(y_i - \hat{y}_i)^2\tag{3}$$

$$SS_{tot} = \sum\limits_{i = 1}^m(y_i - \bar{y}_i)^2\tag{4}$$

2) Mean Absolute Error (MAE) วัดค่าเฉลี่ยของผลรวมความต่างระหว่างค่าจริงกับค่าที่พยากรณ์ได้:

$$MAE = \frac{1}{m} \sum\limits_{i = 1}^m|y_i - \hat{y}_i|\tag{5}$$

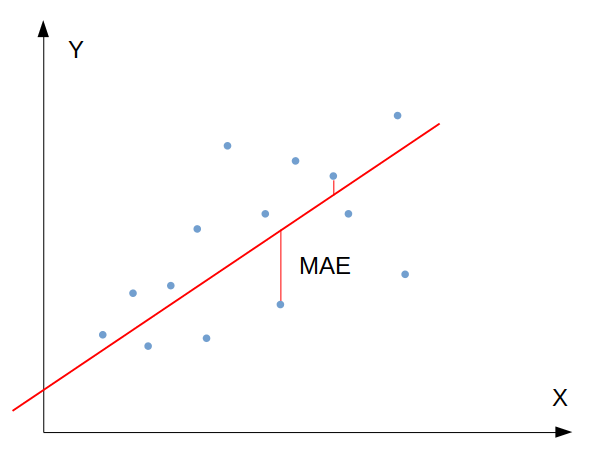
วัดค่าเฉลี่ยของความคลาดเคลื่อนของทั้งโมเดล

3) Mean Squared Error (MSE) วัดค่าเฉลี่ยของผลรวมยกกำลังสองของความต่างระหว่างค่าจริงกับค่าที่พยากรณ์ได้:

$$MSE = \frac{1}{m} \sum\limits_{i = 1}^m(y_i - \hat{y}_i)^2\tag{6}$$

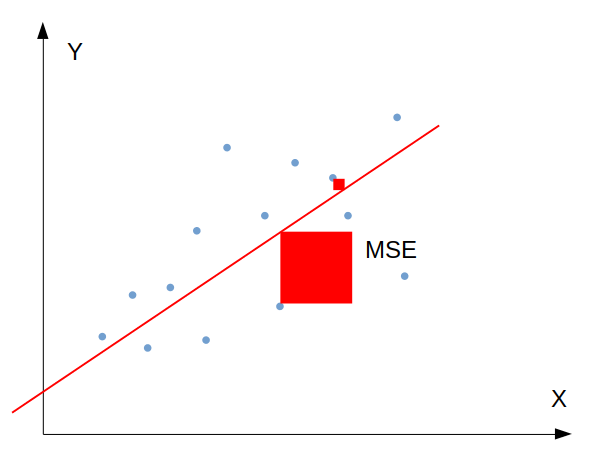
สำหรับ MSE ตัวอย่างบางตัวที่มีความคลาดเคลื่อนระหว่างค่าจริงกับค่าพยากรณ์สูง จะถูกให้ค่าน้ำหนักมากเป็นทวีคูณ ดังนั้น MSE จึงชี้วัดได้ดีว่าโมเดลของเรามีตัวอย่างที่มีค่าความคลาดเคลื่อนสูงผิดปกติหรือไม่ (Sensitive to outliers)

4) Root Mean Squared Error (RMSE) คือ Square root ของ MSE:

$$RMSE = \sqrt{\frac{1}{m} \sum\limits_{i = 1}^m(y_i - \hat{y}_i)^2}\tag{7}$$

RMSE ใช้ Square root แปลง MSE กลับมาให้มีหน่วยใกล้เคียงกับ MAE เพื่อให้ตีความเปรียบเทียบได้ง่ายขึ้น สามารถชี้วัดการกระจายตัวของค่าความคลาดเคลื่อนได้ดี ในกรณีของเราให้ค่าใกล้เคียงกับ MAE คือประมาณ ~ 7-8

จะเห็นว่าโมเดลของเรายังพยากรณ์ได้ไม่ดีนัก ซึ่งมีสาเหตุและทางแก้ดังนี้:

• โมเดลเทรนบนข้อมูลขนาดเล็กมาก คือ Train set 15 รายการเท่านั้น Machine learning ต้องการข้อมูลจำนวนมากกว่านั้นมาก อย่างต่ำๆ ควรจะเป็นหลักหลายๆ ร้อย หรือหลักพัน โดยสำหรับ Linear regression ที่เส้นพยากรณ์เป็นเส้นตรง การที่มีข้อมูลจำนวนมากจะทำให้ค่าความคลาดเคลื่อนโดยเฉลี่ยนั้นลดลง ปัญหานี้เรียกว่าปัญหา Bias ซึ่งตรงข้ามกับปัญหา Variance ที่เป็นโมเดลที่ฟิตกับ Train set มากแต่พยากรณ์ Test set ได้ไม่ดี เราจะพูดถึงปัญหาเหล่านี้ในบทถัดๆ ไป
• ข้อมูลอาจจะมีความแปรผันมากจนสมการเส้นตรง $\hat{y} = w_1x_1 + w_2x_2 + \dots + w_nx_n\ + b$ ไม่สามารถฟิตกับข้อมูลได้ดี ถ้าเรามีข้อมูลมากขึ้น เราอาจะลองพล็อต Scatterplot เพื่อดูรูปร่างความสัมพันธ์ข้อมูล แล้วเปลี่ยนสูตร Algorithm ให้ใช้ Hypothesis function ที่เหมาะสมกับรูปร่างข้อมูลขึ้น เช่น หากพบว่าความสัมพันธ์ใน Scatterplot เป็นเส้นโค้ง อาจพิจารณาใช้ Quadratic function ในรูปแบบ $\hat{y} = w_1x^2_1 + w_2x_2 + \dots + w_nx_n\ + b$ เรียกว่า Polynomial regression ซึ่งสามารถหา Class ใน scikit-learn ใช้ได้

ภาพโดย Skbkekas - Own work, CC BY 3.0

เป็นอันว่าเราสามารถแปลงข้อมูลที่เป็นข้อความหรือหมวดหมู่ให้เป็นตัวเลขได้แล้ว บทต่อไปเราจะพูดถึงการทำ Feature scaling ซึ่งเป็นอีกขั้นตอนของการเตรียมข้อมูล

หน้าแรก | บทที่ 4 Logistic Regression | บทที่ 6 Feature Scaling